Example: Solve the polynomial equation

Solution: Solve the polynomial equation by factoring.
 |
|
|
 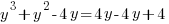 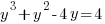 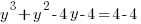 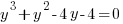 |
|
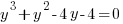 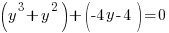 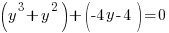 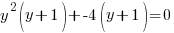 |
|
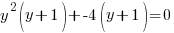 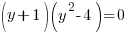 |
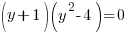 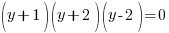 |
|
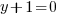 or or 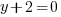 or or 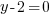 |
|
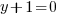 or or 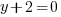 or or 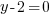 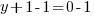 or or 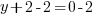 or or 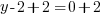 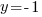 or or 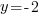 or or 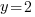 |
The solutions to the polynomial equation  are
are 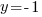 or
or 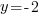 or
or 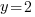 .
.
Example: Solve the polynomial equation

Solution: Solve the polynomial equation by factoring.
 |
|
|
 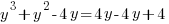 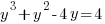 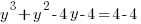 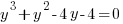 |
|
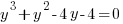 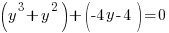 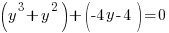 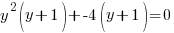 |
|
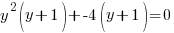 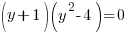 |
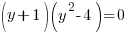 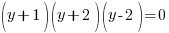 |
|
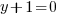 or or 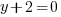 or or 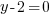 |
|
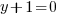 or or 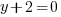 or or 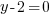 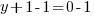 or or 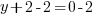 or or 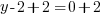 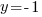 or or 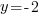 or or 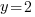 |
The solutions to the polynomial equation  are
are 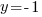 or
or 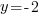 or
or 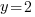 .
.
Example: Solve the quadratic equation with the quadratic formula.
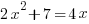
Solution:
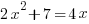 |
|
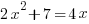 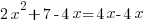 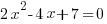 |
|
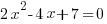 |
|
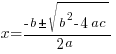 |
|
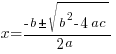 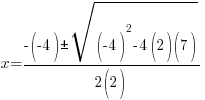 |
|
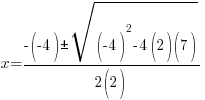 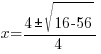 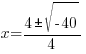 |
|
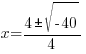 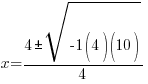 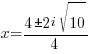 |
|
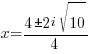 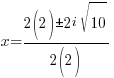 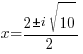 |
The solutions to the quadratic equation are 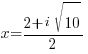 and
and 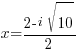 .
.
Example: Solve the quadratic equation by factoring.
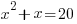
Solution:
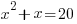 |
|
| Write the equation with all the terms on one side of the equation and zero on the other side of the equation. | 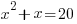 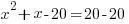 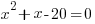 |
| Factor the expression on one side. | 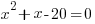 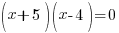 |
| Use the zero product property and set each factor equal to zero. | 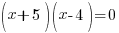 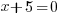 or or 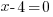 |
| Solve each equation. | 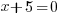 or or 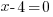 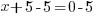 or or 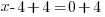 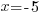 or or 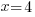 |
Check: 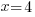
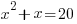
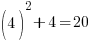
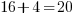
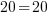
Since the value of 4 makes the equation true, 4 is a solution to the equation.
Check: 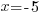
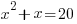
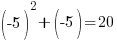
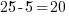
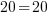
Since the value of -5 makes the equation true, -5 is a solution to the equation.
Example: Solve the quadratic equation by factoring.
 |
|
| The equation already has all of the terms on the same side and zero on the other side. |  |
| Factor the expression on one side. The expression for this equation is a difference of squares. |  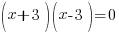 |
| Use the zero product property and set each factor equal to zero. | 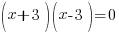 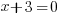 or or 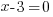 |
| Solve each equation. | 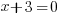 or or 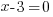 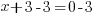 or or 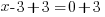 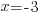 or or 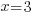 |
Example: Solve the quadratic equation with completing the square.

 |
|
| Rewrite the quadratic equation so that the square and everything that the square applies to are on one side of the equation. This is called isolating the square. |  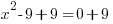 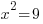 |
| Cancel out the square by square rooting both sides. | 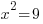 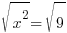 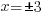 |
| The remaining equations are already solved. The solutions to the equation are 3 and -3. | 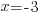 or or 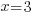 |
Problem: Two pumps were required to pump the water out of a submerged area after a flood. Pump A, the larger of the two pumps, can pump the water out in 24 hours, whereas it would take pump B 120 hours. Both pumps were working for the first 8 hours until pump A broke down. How long did it take pump B to pump the remaining water?
Solution:
Create a table. List each individual and the time it takes to complete the job. Also include a row for the pumps working together. Use a variable to represent the unknown time to complete the job when the pumps are working together.
| 24 hours | ||
| 120 hours | ||
| Together | x |
Fill in the table with the portion of the job completed in one hour.
If it takes Pump A 24 hours to complete the whole job, one twenty-forth (1/24) of the job will be completed in one hour.
If it takes Pump B 120 hours to complete the whole job, one one hundred twentieth (1/120) of the job will be completed in one hour.
If it takes x number of hours when the pumps are working together 1/x portion of the job will be completed in one hour.
| Portion completed in 1 hour | ||
| 24 hours | 1/24 | |
| 120 hours | 1/120 | |
| Together | x | 1/x |
From here an equation can be created with the portion of the job completed in one hour.
In one hour, the portion completed by pump A plus the portion completed by pump B should equal the portion when they are working together.
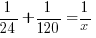
Solve the equation to find x.
| The original equation is a rational equation. | 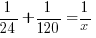 |
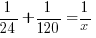 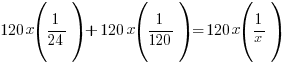 |
|
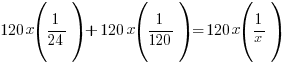 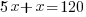 |
|
| Solve the remaining linear equation. | 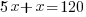 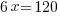 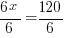 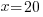 |
It would take both pumps working together 20 hours to pump out all of the water.
But the two pumps are only working together for 8 hours which means they only get eight-twentieths (8/20) of the job done. This fraction reduces to two-fifths (2/5).
Three-fifths (3/5) of the water remains and pump B is working alone.
It takes pump B 120 hours to complete the whole job. It will take 120(3/5) to pump the remaining water out.
120(3/5)= 72 hours.
It takes pump B 72 hours to pump the remaining water.
Example: Solve the inequality. Express the solution using interval notation.
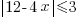
Solution:
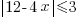 |
|
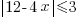 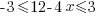 |
|
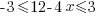 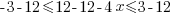 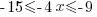 |
|
| Isolating the x in the middle: Divide by -4 on each part. Note: Reverse the inequality symbol when dividing by a negative. Reversing the order of the numbers is equivalent to reversing the signs. |
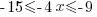 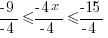 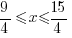 |
| Write the interval notation for the inequality. | ![[9/4,15/4] [9/4,15/4]](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_5fec13cbb1581c25457a13c80c4d3acb.png) |