Category Archives: MAC1105
Perpendicular Lines and Parallel Lines
Example: What are parallel and perpendicular lines?
Example: How are the slopes of parallel and perpendicular lines related? (only watch until 1 min 20 seconds)
Example: Are the lines parallel, perpendicular or neither?
Example: Are the lines perpendicular to each other?
Finding the equation of a line perpendicular to another line
Example: Write the equation of a line in point-slope form passing through the point 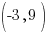 and perpendicular to the line whose equation is
and perpendicular to the line whose equation is 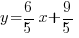 .
.
Solution:
Use the point-slope formula of the line to start building the line. m represents the slope of the line and 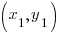 is a point on the line.
is a point on the line.
Point-slope formula: 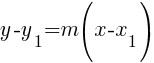
Although the slope of the line is not given, the slope can be deducted from the line being perpendicular to 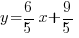 .
.
Perpendicular lines have negative reciprocal slopes. Since the slope of the given line is 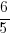 , the slope of the perpendicular line
, the slope of the perpendicular line 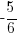 .
.
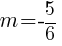 and
and 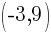
Substitute the values into the point-slope formula.
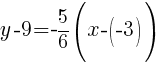
The point-slope form of the line is as follows.
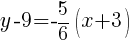
Example: Find the equation of a line perpendicular to another line and passing through a specific point. (The other line in slope intercept form)
Example: Find the equation of a line perpendicular to another line and passing through a specific point. (The other line in slope standard form)
Example: Find the equation of a line perpendicular to the x-axis.
Example: Find the equation of a line perpendicular to the x-axis and perpendicular to the y-axis.
Finding the Equation of a Line parallel to another line
Example: Find the equation of the line parallel to another line and passing through a specific point. (parallel equation in slope intercept form)
Example: Find the equation of the line parallel to another line and passing though a specific point. (parallel line in standard form)
Example: Find the equation of the line parallel to the x-axis or y-axis and passing through a specific point.
Example: What is an equation parallel to the y-axis?
Example: What is an equation parallel to the x-axis?
Finding the Equation of a line given a fractional slope and a point
Example: Find the equation of a line in slope intercept form given the slope of the line is 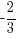 and the line passes through the point
and the line passes through the point 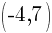
Solution:
Use the point-slope formula of the line to start building the line. m represents the slope of the line and 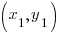 is a point on the line.
is a point on the line.
Point-slope formula: 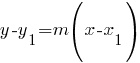
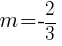 and
and 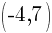
Substitute the values into the formula.
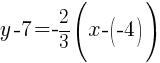
Since the instructions ask to write the equation in slope intercept form 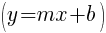 we will simplify and write the equation with y by itself on one side. I will also use the clearing fractions method to avoid having to add fractions.
we will simplify and write the equation with y by itself on one side. I will also use the clearing fractions method to avoid having to add fractions.
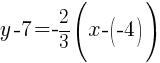
![3(y-7) = 3[-{2/3}(x+4)] 3(y-7) = 3[-{2/3}(x+4)]](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980_0233a6f7265fc4d6a65d52d25e31bbd1.png) (Multiply by LCM)
(Multiply by LCM)
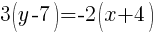 (Cancel Denominator)
(Cancel Denominator)
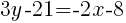
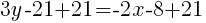
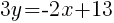
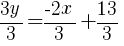
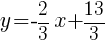
The equation of a line in slope intercept form with a slope of 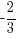 and passing through the point
and passing through the point 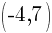 is
is 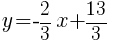
Finding the Equation of a Line given two points on the line
Example: Find the equation of a line in slope intercept form given the line passes through the two points 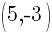 and
and 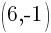 .
.
Solution:
First find the slope of the line.
Choose one of the points to be 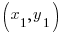 and choose the other point to be
and choose the other point to be 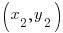 .
.
I will choose 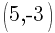 to be
to be 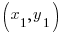 and choose
and choose 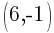 to be
to be 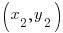 .
.
Substitute these values into the slope formula and simplify.
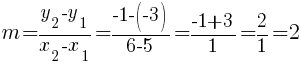
The slope of the line containing the points 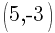 and
and 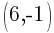 is
is 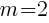 .
.
Then, use the point-slope formula of the line to start building the line. m represents the slope of the line and you can use 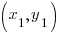 or
or 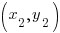 as the point on the line.
as the point on the line.
Point-slope formula: 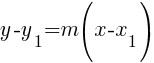
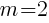 and
and 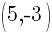
Substitute the values into the formula.
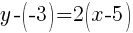
Since the instructions ask to write the equation in slope intercept form 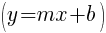 we will simplify and write the equation with y by itself on one side.
we will simplify and write the equation with y by itself on one side.
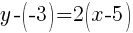
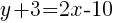
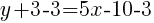
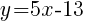
The equation of a line in slope intercept form passing through the two points 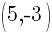 and
and 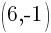 is
is 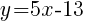 .
.
Finding the Equation of a Line given the slope and a point
Example: Find the equation of a line in slope intercept form given the slope of the line is 7 and the line passes through the point 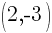
Solution:
Use the point-slope formula of the line to start building the line. m represents the slope of the line and 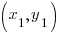 is a point on the line.
is a point on the line.
Point-slope formula: 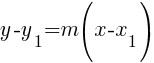
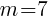 and
and 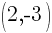
Substitute the values into the formula.
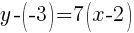
Since the instructions ask to write the equation in slope intercept form 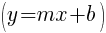 we will simplify and write the equation with y by itself on one side.
we will simplify and write the equation with y by itself on one side.
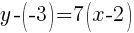
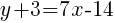
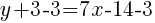
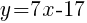
The equation of a line in slope intercept form with a slope of 7 and passing through the point 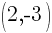 is
is 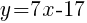 .
.
Example: Find the equation of the line.
X-intercepts and Y-intercepts
An x-intercept is where the graph touches or crosses the x-axis.
A y-intercept is where the graph touches of crosses the y-axis.
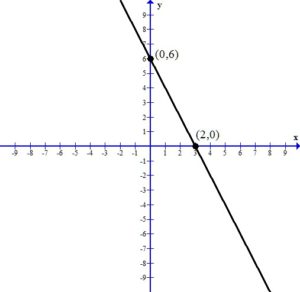
In this picture, the graph crosses the x-axis at the ordered pair 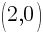 . Since every ordered pair on the x-axis has a y coordinate of zero we can let
. Since every ordered pair on the x-axis has a y coordinate of zero we can let  to find x-intercepts.
to find x-intercepts.
To find an x-intercept: Let y=0 and solve for x.
In this picture, the graph crosses the y-axis at the ordered pair 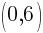 . Since every ordered pair on the y-axis has a x coordinate of zero we can let
. Since every ordered pair on the y-axis has a x coordinate of zero we can let 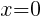 to find y-intercepts.
to find y-intercepts.
To find an y-intercept: Let x=0 and solve for y.
Graphing Linear Equations by Finding Intercepts
Steps for Graphing with the Intercept Method
- Find the x intercept and the y-intercept.
- To find an x-intercept let y=0 and solve for x.
- To find a y-intercept let x=0 and solve for y.
- Plot the x-intercept and y-intercept.
- Draw the line that connects the intercepts.
Example: Graph the linear equation 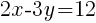
Solution:
1. Find the x-intercept and the y-intercept.
To find an x-intercept: Let y=0 and solve for x.
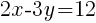
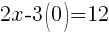
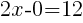
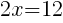
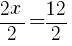
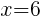
The x-intercept of this equation is 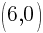
To find a y-intercept: Let x=0 and solve for y.
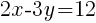
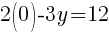
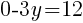
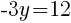
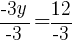
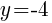
The y-intercept of this equation is 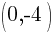
2. Plot the x-intercept and the y-intercept.
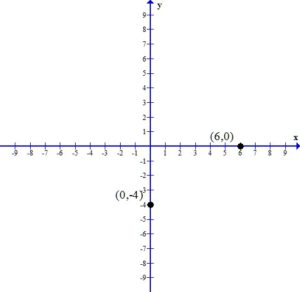
3. Draw the line that connects the intercepts.
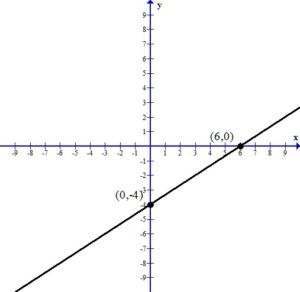
Example: Graph the linear equation 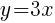
Solution:
1. Find the x-intercept and the y-intercept.
To find an x-intercept: Let y=0 and solve for x.
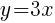
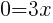
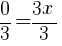
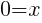
The x-intercept of this equation is 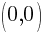
To find a y-intercept: Let x=0 and solve for y.
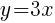
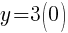
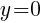
The y-intercept of this equation is 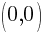
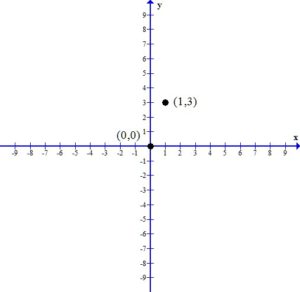
Since the x-intercept and the y-intercept are the same point and we need two distinct points to graph a line, we must find another ordered pair that is a solution to the equation.
Let x=1 and find the associated y value. (I chose x=1 but you could choose a different value)
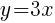
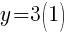
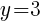
Another ordered pair on the graph is 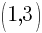
2. Plot the x-intercept and the y-intercept.
3. Draw the line that connects the intercepts.
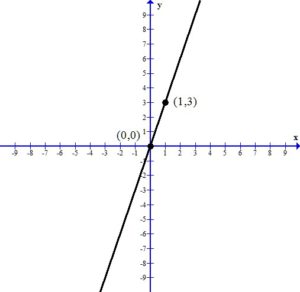
Example: Graphing a linear equation with intercepts.
Example: Graphing a linear equation with intercepts.
Example: Graphing a linear equation with intercepts.
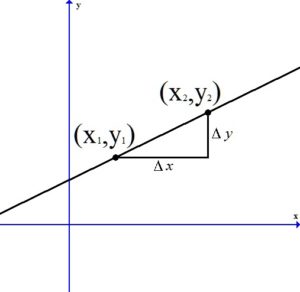
Calculating Slope
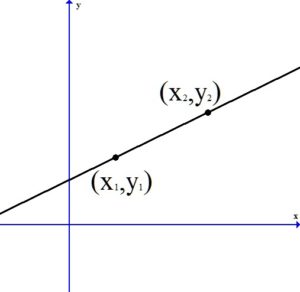
Given two points on the line 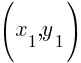 and
and 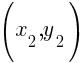 , you can calculate the slope of a line by the following formula.
, you can calculate the slope of a line by the following formula.
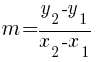
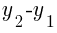 is also know as
is also know as 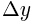 or “the change in y.”
or “the change in y.”
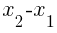 is also know as
is also know as 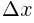 or “the change in x.”
or “the change in x.”
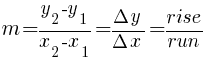
Example: Calculate the slope of the line containing the points 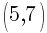 and
and 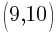 .
.
Solution: Choose one of the points to be 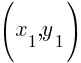 and choose the other point to be
and choose the other point to be 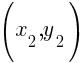 .
.
I will choose 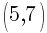 to be
to be 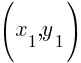 and choose
and choose 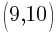 to be
to be 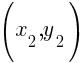 .
.
Substitute these values into the slope formula and simplify.
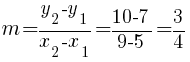
The slope of the line containing the points 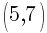 and
and 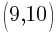 is
is 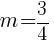 .
.
Example: Calculate the slope of the line containing the points 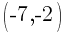 and
and 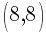 .
.
Solution: Choose one of the points to be 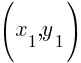 and choose the other point to be
and choose the other point to be 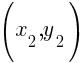 .
.
I will choose 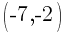 to be
to be 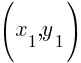 and choose
and choose 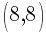 to be
to be 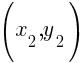 .
.
Substitute these values into the slope formula and simplify.
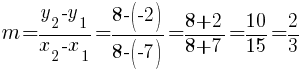
The slope of the line containing the points 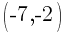 and
and 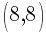 is
is 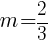 .
.
Example: Finding the slope with the formula.
https://www.youtube.com/watch?v=1Cm7hjMUsrQ
Example: Finding the slope with the formula.
Example: Finding the slope from the graph.