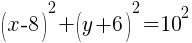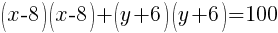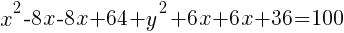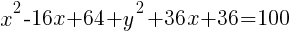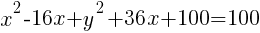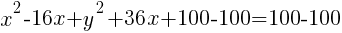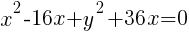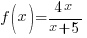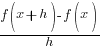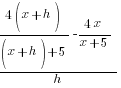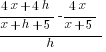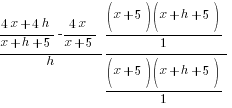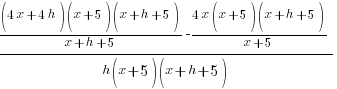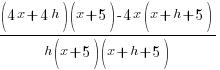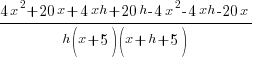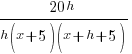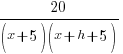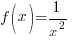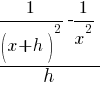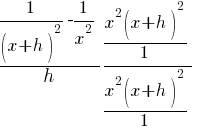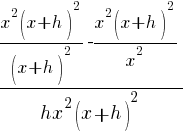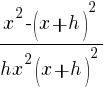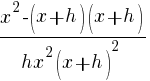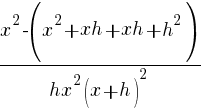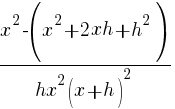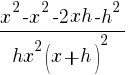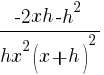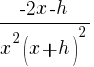Example: Solve the equation.
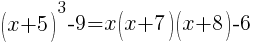
Solution:
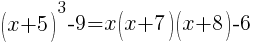 |
|
| Simplify both sides of the equation. On the left hand side, rewrite the exponent. On the right hand side, begin to simplify the multiplication. | 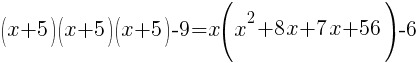 |
| Simplify both sides of the equation. On the left hand side, begin multiplying. On the right hand side, combine like terms. | 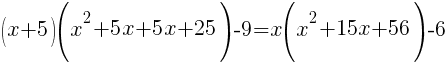 |
| Simplify both sides of the equation. On the left hand side, combine like terms. On the right hand side use the distributive property. | 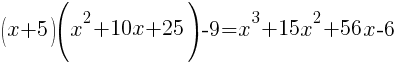 |
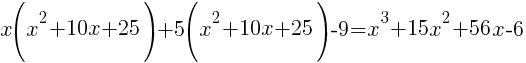 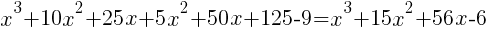 |
|
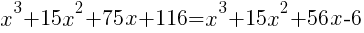 |
|
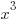 from each side. It cancels from each side. from each side. It cancels from each side. |
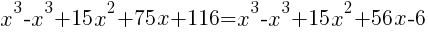 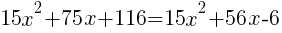 |
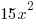 from each side. It cancels from each side. from each side. It cancels from each side. |
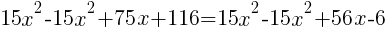 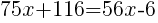 |
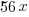 from each side and simplify. from each side and simplify. |
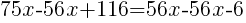 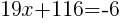 |
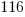 from each side and simplify. from each side and simplify. |
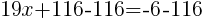 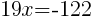 |
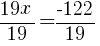 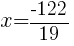 |
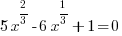
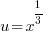
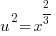
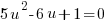
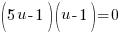
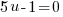 or
or 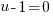
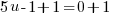 or
or 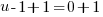
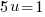 or
or 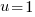
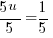 or
or 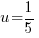 or
or 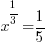 or
or 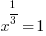
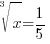 or
or 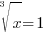
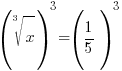 or
or 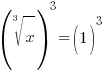
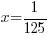 or
or