Practice Problems
Addition and Multiplication Principles Combined
Solutions to Practice Problems
Example: Rewrite the expression in the form 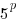 where p is an algebraic expression.
where p is an algebraic expression.
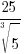
Solution:
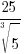 |
|
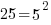 |
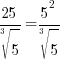 |
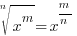 . For this example . For this example 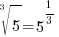 |
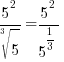 |
Quotient Rule for Exponents 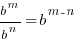 |
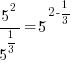 |
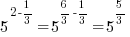 |
Example: Classify the function as a polynomial function, rational function, or root function, and then find the domain. Write the domain interval notation and set builder notation.
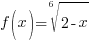
Solution:
Classify the Function
| Polynomial Function
A polynomial function is a function of the form
where n is a non-negative integer {0, 1, 2, 3, 4, …} and the coefficients |
|
| Rational Function
A rational function is a function of the form
where |
|
| Root Function (even index)
A root function is a function of the form
where n is an even positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an even number. {2, 4, 6, 8, …} The square root is an even index although the index is not written. |
| Root Function (odd index)
A root function is a function of the form
where n is an odd positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an odd number. {3, 5, 7, 9, …} The cube root is an odd index. |
Since the function 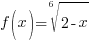 has a radical and the index is even. This function is a root function.
has a radical and the index is even. This function is a root function.
Find the Domain of a Root Function (Even Index)
Taking the even root of a negative number results in a complex or imaginary number. Since we are interested in real function values, we would like the expression inside the radical to be non-negative ( zero or positive) The root function is defined for any value of the variable where the expression under the radical is non-negative (zero or positive). Find these values by creating an inequality to solve. The inequality is the expression under the radical greater than or equal to zero.
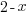 |
|
| Solve the inequality. This inequality is a linear inequality and can be solved by isolating the variable on one side. | 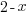 |
| Solve by isolating the variable. Start by subtracting 2 on both sides. | 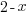 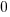 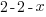 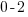 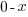 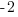 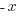 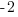 |
| Isolate the variable. Continue by dividing both sides by -1. Be sure to reverse the inequality symbol since you are dividing both sides by a negative. | 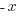 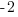 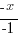 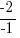 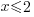 |
The function values where 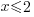 are defined for
are defined for 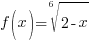 .
.
In set builder notation, the domain is ![]() .
.
In interval notation, the domain is (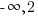 ]
]
Example:
How long does it take for an investment to double if it is invested at 18% compounded continuously?
Solution:
Since this question involve continuous compound interest, we will use the associated formula.
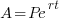
We are given that the interest rate is 18% or 0.18. This tells me that when r=0.18 Since we are looking for the doubling time, A will be 2 times P. I can write that in symbols A=2P.
Substitute these values into the continuous compound formula and solve for the interest rate.
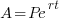 |
|
| Substitute the values of r and A into the formula | 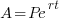 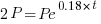 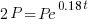 |
| Solve for t by dividing both sides by P and simplifying | 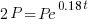 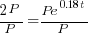 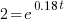 |
| Solve for t by taking the log of both sides. | 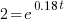 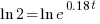 |
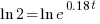 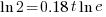 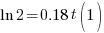 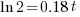 |
|
| Solve for t by dividing both sides by 0.18 and simplifying | 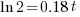 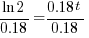 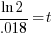 |
| Find the value in the calculator | 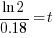 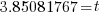 |
| Write the answer rounded to two decimal places | 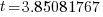 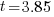 |
It will take 3.85 years to double your money when interest is compounded continuously at 18%.
If you need to write this in years and months, you will need to convert the 0.85 to months. Since there are 12 months in a year, multiply 0.85 by 12 to get 10.2. I will round to the nearest months to get 10.
It will take 3 years and 10 months to double your money when interest is compounded continuously at 18%.
Here is a video that is similar except that you are looking for the investment to triple.
Example: Given the quadratic function in vertex form, state the domain, range, vertex, x-intercepts, y-intercept, the orientation (opens up or opens down), and the axis of symmetry. Finally graph the function.
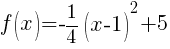
Solution:
Find the vertex.
When the quadratic function is written in standard form you can identify the vertex as (h,k).
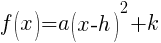
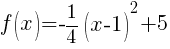
The vertex of the quadratic function is 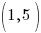 .
.
Find the orientation.
The leading coefficient of the quadratic function is negative so the parabola opens down.
Find the y-intercept.
To find a y-intercept let x=0.
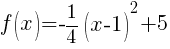 |
|
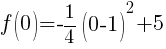 |
|
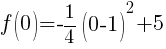 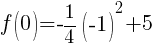 |
|
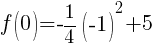 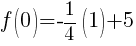 |
|
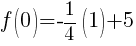 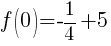 |
|
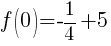 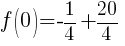 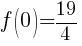 |
The y-intercept is 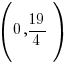 .
.
Find the x-intercept.
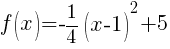 |
|
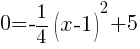 |
|
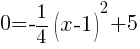 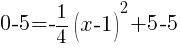 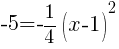 |
|
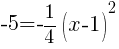 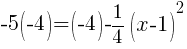 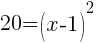 |
|
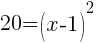 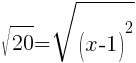 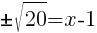 |
|
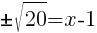 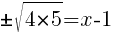 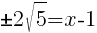 |
|
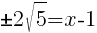 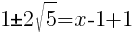 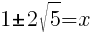 |
|
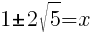 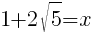 or or 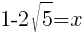 |
The x-intercepts are 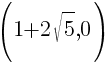 and
and 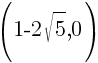
Find the axis of symmetry.
The axis of symmetry is a vertical line that passes through the vertex. Since the vertex is 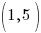 the axis of symmetry is
the axis of symmetry is  .
.
Graph the function.
Plot the intercepts and the vertex.
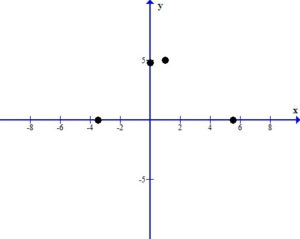
Since the vertex is the highest point we can draw the parabola using the peak at the vertex.
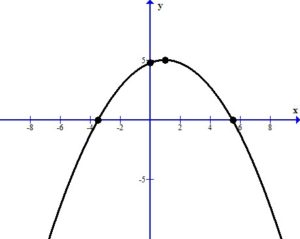
Find the domain and range.
The domain is 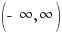 .
.
The range is 
![- infty, 5 {}{]} - infty, 5 {}{]}](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_d4fedb3b6ae0adccbd6fd0360d594d3c.png) .
.
Here is a video example analyzing a quadratic function in vertex form.
Problem:
A 28 inch wire is to be cut. One piece is to be bent into the shape of a square, whereas the other piece is the bent into the shape of a rectangle whose length is twice the width. Find the width of the rectangle that will minimize the total area.
Solution:
First draw a picture of the shapes the wire will make and label the sides.
The square has equal sides. Label the side as an unknown quantity x.
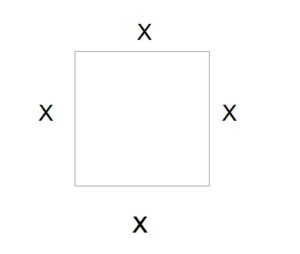
The perimeter of the square is 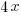 and the area of the square is
and the area of the square is 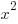 .
.
The rectangle described as a length that is twice the width. Label the sides as y and 2y.

The perimeter of the rectangle is 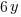 and the area of the rectangle is
and the area of the rectangle is 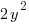 .
.
Since the 28 inch piece of wire will be cut and used to form the square and rectangle the total perimeter of the two shapes is 28 inches.
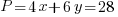
The total area is to be minimized.
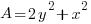
To minimize the area there must be only one variable in the expression. Use the perimeter equation to reduce the number of variables.
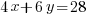 |
|
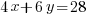 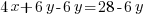 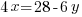 |
|
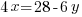 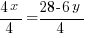 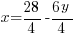 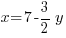 |
Substitute into the area expression to reduce from having two variables to have one variable.
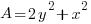 |
|
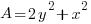 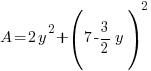 |
|
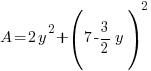 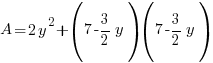 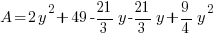 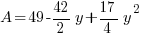 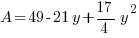 |
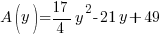 is in the form of a quadratic function. The graph of a quadratic function is a parabola. This quadratic function has a leading coefficient of
is in the form of a quadratic function. The graph of a quadratic function is a parabola. This quadratic function has a leading coefficient of 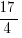 and since it is positive means that the parabola is opening up.
and since it is positive means that the parabola is opening up.
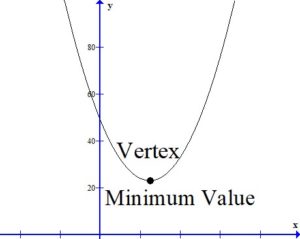
Find the vertex to find the minimum value.
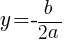 |
|
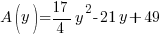 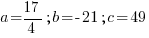 |
|
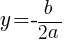 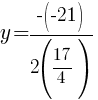 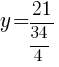 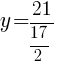 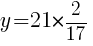 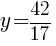 |
|
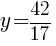 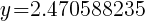 |
Round to the nearest tenth and 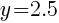 .
.
The total area of the square and rectangle is minimized when the width of the rectangle is 2.5 inches.
Example: For the function below. Graph using transformations.
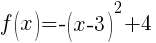
First we must examine the base function 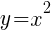
Graph using plotting points. We can use the standard set of x-values to find ordered pairs. Substitute the standard set of x-values into the base function to get the base graph.
| x | y |
|---|---|
| -2 | (-2)^2=4 |
| -1 | (-1)^2=1 |
| 0 | (0)^2=0 |
| 1 | (1)^2=1 |
| 2 | (2)^2=4 |
The graph below shows the points plotted and the line that connects them. The domain is 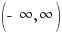 and the range is [
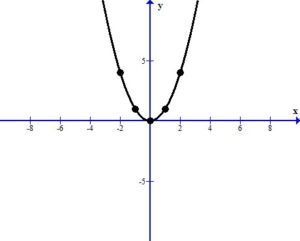
and the range is [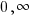 )
)
Analyze the transformations.
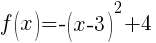
The -3 inside the square shifts the graph right 3 units.
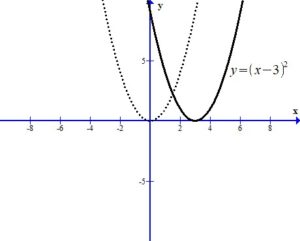
The – in the front of the base reflects the graph over the x-axis.
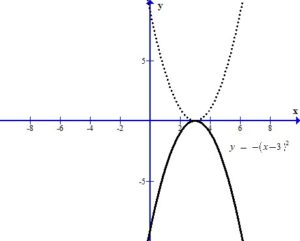
The +4 outside the square shifts the graph up 4 units.
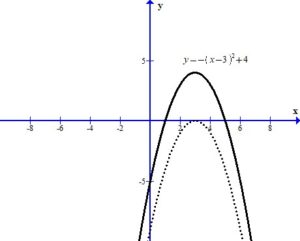
You can see the graph after the transformations.
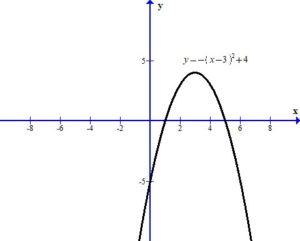
The domain is 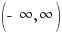 and the range is (
and the range is (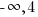 ]
]
Here is a video example of a transformation of a square function.