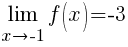The function f below is undefined for x=-1. Using a table, analyze what is happening to f(x) as x approaches -1.
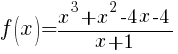
Filling out this table will help us decide what is happening to f(x) as x is getting closer to -1 from the left. (x’s that are smaller then -1)
| x | -1.1 | -1.01 | -1.001 | -1.0001 | -1 |
| f(x) | ? |
Filling out this table will help us decide what is happening to f(x) as x is getting closer to -1 from the right. (x’s that are larger then -1)
| x | -.9 | -.99 | -.999 | -.9999 | -1 |
| f(x) | ? |
Here is a video that will help you use the features in your calculator to fill in the values of the table:
| x | -1.1 | -1.01 | -1.001 | -1.0001 | -1 |
| f(x) | -2.79 | -2.9799 | -2.998 | -2.9998 | ? |
As you can see from the table, f(x) approaches -3 as x approaches -1 from the left. Symbolically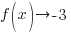 
as 
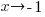from the left would be written.
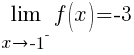
| x | -.9 | -.99 | -.999 | -.9999 | -1 |
| f(x) | -3.19 | -3.0199 | -3.002 | -3.0002 | ? |
As you can see from the table, f(x) approaches -3 as x approaches -1 from the right. Symbolically 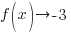as 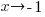from the right would be written.
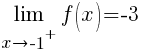
These are called one sided limits.
Informal Definition of a Limit: If f(x) becomes arbitrarily close to a single number L as x approaches c from either side, then the limit of f(x) , as x approaches c is L.
In general: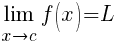 
In our example, f(x) becomes arbitrarily close to -3 as x approaches -1 from the left and right.
