Category Archives: Graphically

Graphically

Limit at a Hole

Use the graph, estimate the limit as x approaches -1.

f(x) = {x^3+x^2-4x-4}/{x+1}

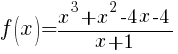
The function f above is undefined for x=-1. By simplifying f(x) we find a function whose graph agrees with f(x) at every point except -1.

f(x) = {x^3+x^2-4x-4}/{x+1}

{= {x^2(x+1)-4(x+1)}/{x+1} }

{={(x^2-4)(x+1)}/{x+1}}

{=x^2-4}

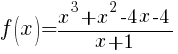
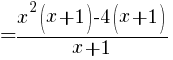
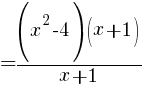
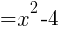
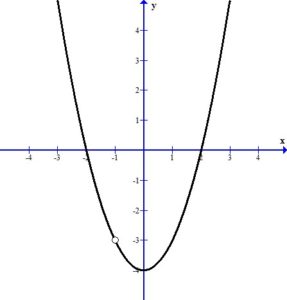
Since f(x) is undefined for x=-1 and we were able to cancel a common factor of x+1 from the numerator and denominator there is a hole in the graph of f(x) at x=-1

Graph with hole

 

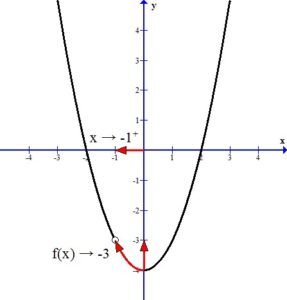
For f(x) to have a limit as x approaches -1 the one-sided limits must agree.

From the right:

Graph with hole right limit

lim{x right -1^{+}}{f(x)}=-3

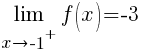
From the left:

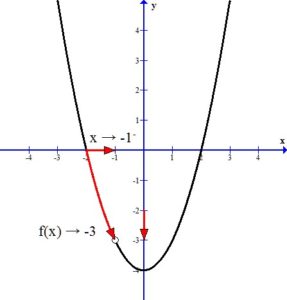
Graph with hole left limit

lim{x right -1^{-}}{f(x)}=-3

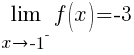
Since the one-sided limits agree, the limit exists.

lim{x right -1}{f(x)}=-3

 

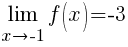
Here are some practice problems.

MAC2311 Limits Graphically