Example: Find the general form of the circle
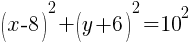
Solution:
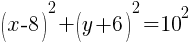
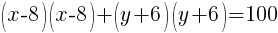
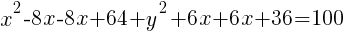
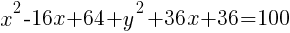
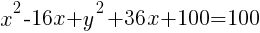
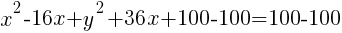
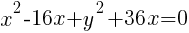
Example: Find the general form of the circle
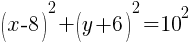
Solution:
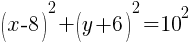
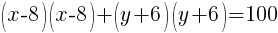
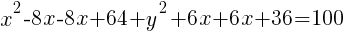
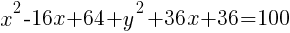
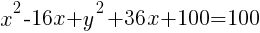
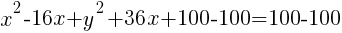
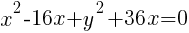
Example: Write the equation of a circle in standard form.
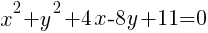
Start by grouping the x terms together, grouping the y terms together and moving the constant to the other side of the equation.
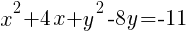
Use completing the square on the group of x terms and the group of y terms.
To find the number that completes the square for the x group, start with the coefficient of the x term, half it and square it. The coefficient of the x term is 4
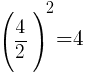
To find the number that completes the square for the y group, start with the coefficient of the y term, half it and square it. The coefficient of the y term is -8
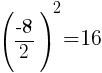
Add these numbers to the group of x terms and the group of y terms. Be careful to maintain the balance of the equation by adding the numbers to both sides of the equation.
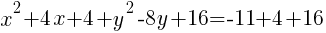
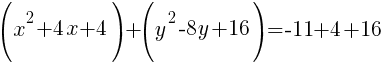
Now the group of x terms is a perfect square trinomial and will factor to be a binomial squared. The group of y terms will do the same.
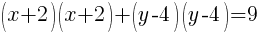
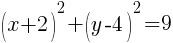
The equation of the circle is written in standard form where it is easy to recognize the center and radius of the circle.
The center is (-2,4) and the radius is 9.
An x-intercept is where the graph touches or crosses the x-axis.
A y-intercept is where the graph touches of crosses the y-axis.
To find an x-intercept: Let y=0 and solve for x.
To find an y-intercept: Let x=0 and solve for y.
Example: Find the intercepts of the circle for the given equation.
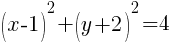
Solution:
To find an x-intercept, let y=0 and solve for x.
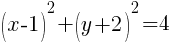
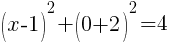
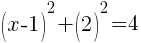
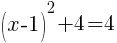
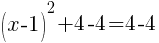
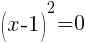
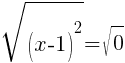
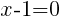
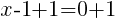
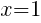
This equation has one x-intercept. 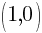
To find a y-intercept, let x=0 and solve for y.
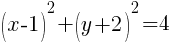
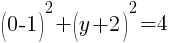
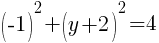
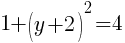
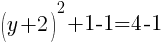
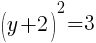
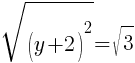
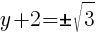
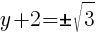
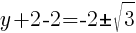
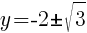
Approximately 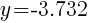 and
and 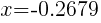
This equation has two y-intercepts. 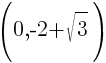 and
and 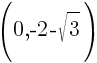
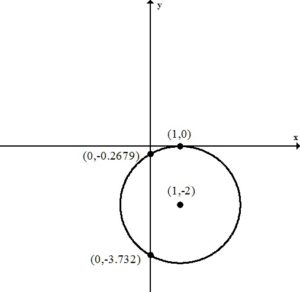
A tangent line to a circle may be defined as a line that intersects the circle in a single point.
This circle is tangent to the x-axis since it is touching the x-axis in a single point. The x-axis (y=0) is the tangent line for the point on the circle (1,0).
Example: Find the intercepts of the circle for the given equation.
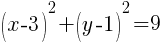
Solution:
To find an x-intercept, let y=0 and solve for x.
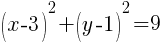
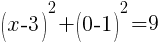
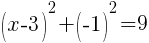
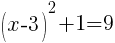
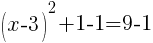
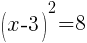
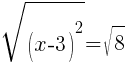
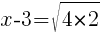
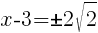
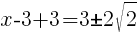
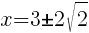
Approximately 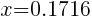 and
and 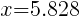
This equation has two x-intercepts. 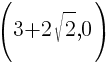 and
and 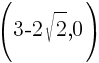
To find a y-intercept, let x=0 and solve for y.
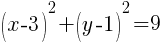
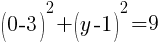
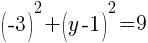
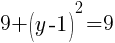
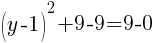
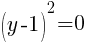
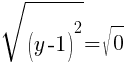
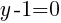
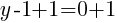
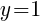
This equation has one y-intercept. 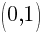 .
.
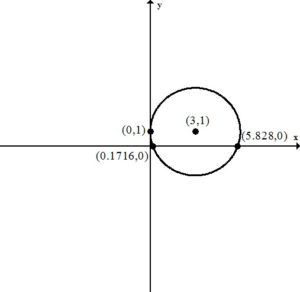
This circle is tangent to the y-axis since it is touching the y-axis in a single point. The y-axis (x=0) is the tangent line for the point on the circle (0,1).
An x-intercept is where the graph touches or crosses the x-axis.
A y-intercept is where the graph touches of crosses the y-axis.
To find an x-intercept: Let y=0 and solve for x.
To find an y-intercept: Let x=0 and solve for y.
Example: Find the intercepts of the circle for the given equation.
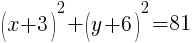
Solution:
To find an x-intercept, let y=0 and solve for x.
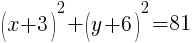
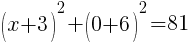
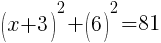
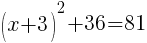
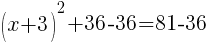
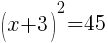
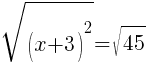
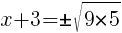
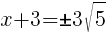
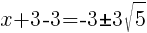
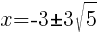
Approximately 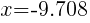 and
and 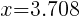
This equation has two x-intercepts. 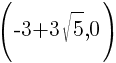 and
and 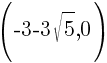
To find a y-intercept, let x=0 and solve for y.
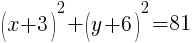
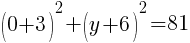
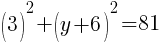
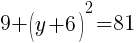
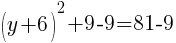
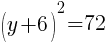
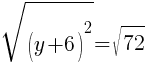
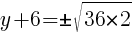
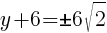
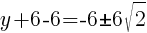
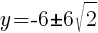
Approximately 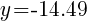 and
and 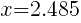
This equation has two y-intercepts. 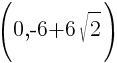 and
and 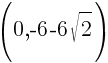
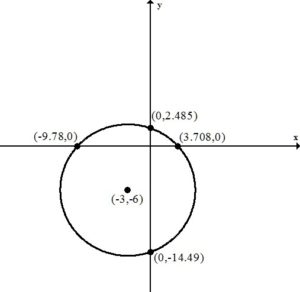
An x-intercept is where the graph touches or crosses the x-axis.
A y-intercept is where the graph touches of crosses the y-axis.
To find an x-intercept: Let y=0 and solve for x.
To find an y-intercept: Let x=0 and solve for y.
Example: Find the intercepts of the circle for the given equation.
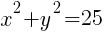
Solution:
To find an x-intercept, let y=0 and solve for x.
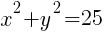
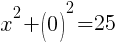
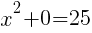
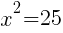
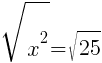
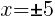
This equation has two x-intercepts. 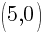 and
and 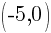
To find a y-intercept, let x=0 and solve for y.
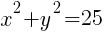
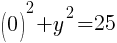
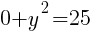
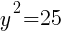
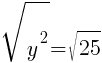
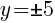
This equation has two y-intercepts. 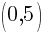 and
and 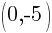
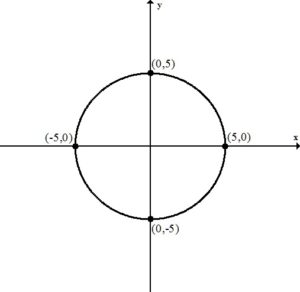
Example: Write the equation of a circle in standard form given the center of the circle is (5,7) and the radius of the circle is 6. Then write the equation in general (expanded) form.
Solution:
The standard form of an equation of a circle is 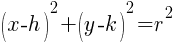 where r is the radius and
where r is the radius and 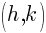 is the center.
is the center.
The center of our circle is 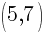 . So
. So 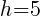 and
and 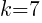 .
.
The radius of our circle is 6 so 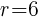 .
.
Replace h, k and r in standard form of an equation of a circle.
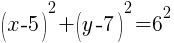
Simplify.
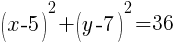
The equation of a circle in standard for with center (5,7) and a radius of 6 is 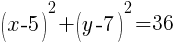 .
.
To write the equation in general form we can start with the standard form we just found and multiply each binomial.
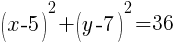
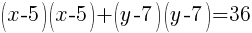
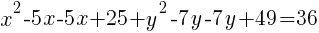
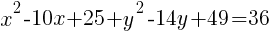
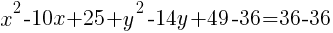
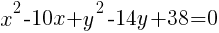
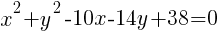
The equation of a circle in general form with center (5,7) and a radius of 6 is 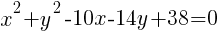 .
.
A circle is the collection of points that are equidistant to a center point. The distance is the radius denoted r. The center is denoted 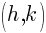 .
.
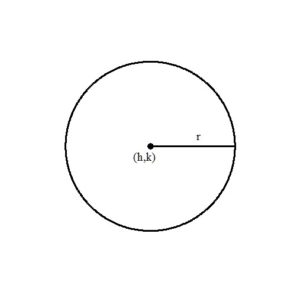
The standard form of an equation of a circle is 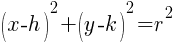 where r is the radius and
where r is the radius and 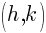 is the center.
is the center.
Example: Find the center and the radius from the given equation.
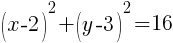
Solution: If you line up the standard form of a circle with the equation given you can determine the center and the radius.
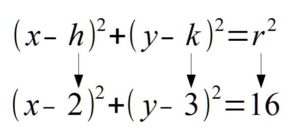
In the binomial with x, the number after the minus sign is h. Thus, 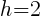 . In the binomial with y, the number after the minus sign is k. Thus,
. In the binomial with y, the number after the minus sign is k. Thus, 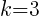 . The
. The 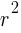 lines up with 16. So
lines up with 16. So 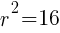 which means
which means 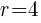 .
.
This is the equation of a circle with a center of 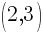 and a radius of
and a radius of 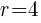 .
.
Example: Find the center and the radius from the given equation.
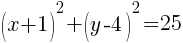
Solution: Notice that one of the binomials has a + instead of the – that is in the standard form of the circle. Rewrite the addition as subtraction.
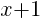 is the same as
is the same as 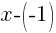 .
.
The rewritten equation is as follows.
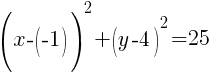
Then, if you line up the standard form of a circle with the equation given you can determine the center and the radius.
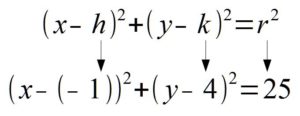
In the binomial with x, the number after the minus sign is h. Thus, 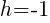 . In the binomial with y, the number after the minus sign is k. Thus,
. In the binomial with y, the number after the minus sign is k. Thus, 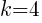 . The
. The 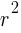 lines up with 25. So
lines up with 25. So 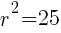 which means
which means 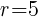 .
.
This is the equation of a circle with a center of 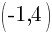 and a radius of
and a radius of 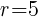 .
.
Example: Find the center and the radius from the given equation.
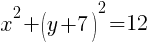
Solution: Notice that one of the binomials has a + instead of the – that is in the standard form of the circle. Rewrite the addition as subtraction.
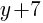 is the same as
is the same as 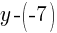 .
.
The other binomial doesn’t have any number added or subtracted. We can rewrite this by subtracting zero.
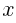 is the same as
is the same as 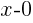 .
.
The rewritten equation is as follows.
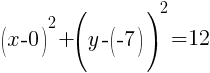
Then, if you line up the standard form of a circle with the equation given you can determine the center and the radius.
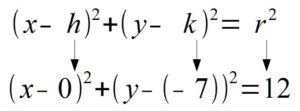
In the binomial with x, the number after the minus sign is h. Thus, 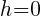 . In the binomial with y, the number after the minus sign is k. Thus,
. In the binomial with y, the number after the minus sign is k. Thus, 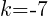 . The
. The 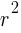 lines up with 25. So
lines up with 25. So 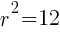 which means
which means 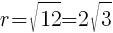 .
.
This is the equation of a circle with a center of 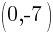 and a radius of
and a radius of 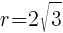 .
.