Example: Rewrite the given quadratic function in standard form by completing the square. Then state the domain, range, vertex, x-intercepts, y-intercept, the orientation (opens up or opens down), and the axis of symmetry. Finally graph the function.
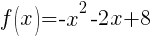
Solution:
Rewrite function in standard form.
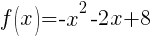
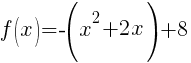
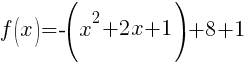
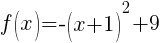
Here is a youTube video that demonstrations the process.
Find the vertex.
When the quadratic function is written in standard form you can identify the vertex as (h,k).
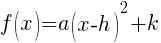
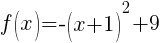
The vertex of the quadratic function is 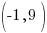 .
.
Find the orientation.
The leading coefficient of the quadratic function is negative so the parabola opens down.
Find the y-intercept.
To find a y-intercept let x=0.
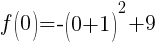
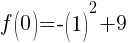
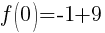
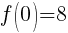
The y-intercept is (0,8).
Find the x-intercept.
To find an x-intercept let y=0 or f(x)=0.
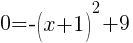
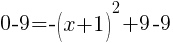
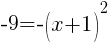
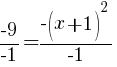
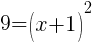
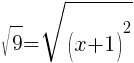
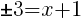
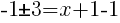
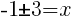
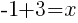 or
or 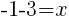
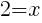 or
or 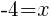
Find the axis of symmetry.
The axis of symmetry is a vertical line that passes through the vertex. Since the vertex is 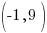 the axis of symmetry is
the axis of symmetry is 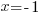 .
.
Graph the function.
Plot the intercepts and the vertex.
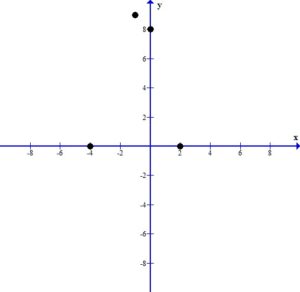
Since the vertex is the highest point we can draw the parabola using the peak at the vertex.
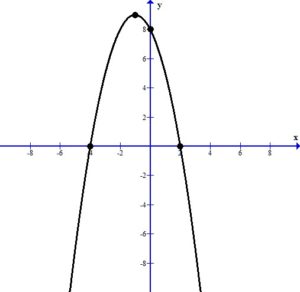
Find the domain and range.
The domain is 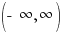 .
.
The range is 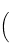
![- infty, 9 {}{]} - infty, 9 {}{]}](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_cf307bba3f49c962fc8d40a950c676b1.png) .
.
Here a few video examples of analyzing the graph in general form.