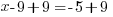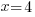Category Archives: Exponential Equations

5.4 Exponential and Logarithmic Equations, 6.6 Logarithmic and Exponential Equations, Exponential Equations

Solve an exponential equation: Take the log of both sides

Example:

(1.41)^x = (sqrt{2})^{1-4x}

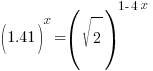
Solution:

 

The exponential equation
 (1.41)^x = (sqrt{2})^{1-4x}
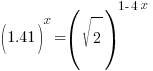Since the bases cannot be easily written the same use the method of taking the log of both sides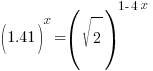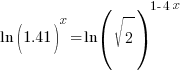
(1.41)^x = (sqrt{2})^{1-4x}
ln (1.41)^x = ln (sqrt{2})^{1-4x}
Use the power rule for logarithms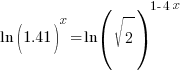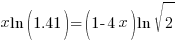
ln (1.41)^x = ln (sqrt{2})^{1-4x}
x ln (1.41) = (1-4x) ln sqrt{2}
Use the distributive law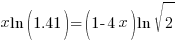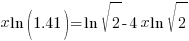
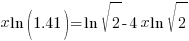x ln (1.41) = (1-4x) ln sqrt{2}
x ln (1.41) = ln sqrt{2}-4x ln sqrt{2}
Collect the terms with x to one side and collect the terms without x on the other side
x ln (1.41) = ln sqrt{2}-4x ln sqrt{2}
x ln (1.41) +4x ln sqrt{2}= ln sqrt{2}-4x ln sqrt{2} +4x ln sqrt{2}
x ln (1.41) +4x ln sqrt{2}= ln sqrt{2}
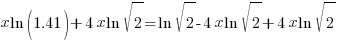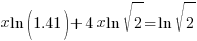Factor the common x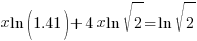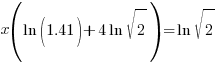
x ln (1.41) +4x ln sqrt{2}= ln sqrt{2}
x( ln (1.41) +4 ln sqrt{2})= ln sqrt{2}
Solve for x by dividing both sides by the factor in the parenthesis and simplify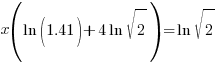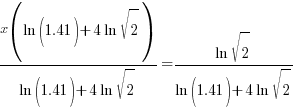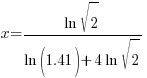
x( ln (1.41) +4 ln sqrt{2})= ln sqrt{2}
{x( ln (1.41) +4 ln sqrt{2})}/{ ln (1.41) +4 ln sqrt{2}}= {ln sqrt{2}}/{ ln (1.41) +4 ln sqrt{2}}
x = {ln sqrt{2}}/{ ln (1.41) +4 ln sqrt{2}}
The solution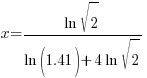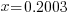
x = {ln sqrt{2}}/{ ln (1.41) +4 ln sqrt{2}}
x =0.2003

When you type this into a calculator be sure to use parenthesis around the numerator and around the denominator.  Here is an example of how you might enter it.

(ln (sqrt{2}))/(ln(1.41)+4 ln(sqrt{2}))

Here is a youtube video with a similar example.

5.1 Exponential Functions, 6.6 Logarithmic and Exponential Equations, Exponential Equations

Solving an Exponential Equation: Relating the Bases

Example:  Solve the exponential equation.

4^{x-9}=1/1024

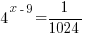
Solution:

The exponential equation
4^{x-9}=1/1024
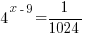Try to write both sides of the equation with the same base.  Try 4 since there is a base of 4 on the left 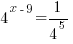4^{x-9}=1/4^5
Using a property of negative exponents move the base to the numerator  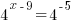4^{x-9}=4^{-5}
Now that that the bases are the same the exponents must be equal  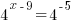4^{x-9}=4^{-5}

x-9=-5
Solve for x
  x-9=-5

x-9+9=-5+9

x=4

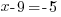
The solution the the exponential equation is 4.

Here is a youtube video with a similar example.