Example: Solve the equation.
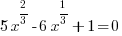
Solution:
The equation is similar to a quadratic. It has 3 terms and one exponent is twice the other. Since the equation is quadratic in form, use substitution to solve the equation.
Use the following substitution to rewrite the equation
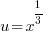
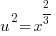
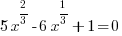 |
|
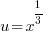 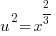 |
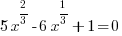 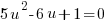 |
1) Factor the quadratic |
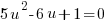 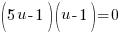 |
2) Apply the zero product property |
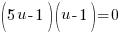 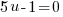 or or 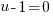 |
3) Solve each linear factor |
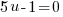 or or 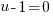 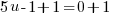 or or 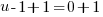 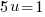 or or 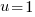 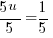 or or 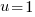 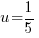 or or 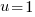 |
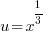 |
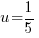 or or 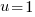 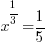 or or 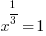
|
| Solve the equation with rational exponents. 1) Rewrite the rational exponents in radical form |
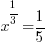 or or 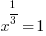 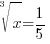 or or 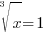 |
| Solve the equation with rational exponents. 2) Cancel the cube root by cubing both sides. 3) Simplify |
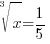 or or 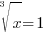 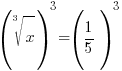 or or 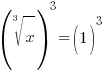 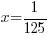 or or  |
The solution to 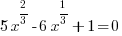 is
is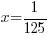 or
or  .
.
Here is a video with similar examples.