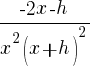Example: Find the difference quotient for 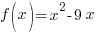
The Difference Quotient: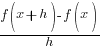
Solution:
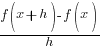 |
|
| Write the difference quotient for the given function | 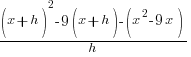 |
| Apply the exponent and use the distributive property | 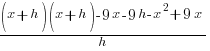 |
| Multiply | 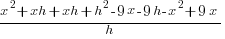 |
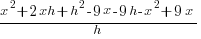 |
|
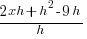 |
|
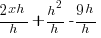 |
|
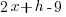 |
Example: Find the difference quotient for 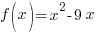
The Difference Quotient: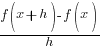
Solution:
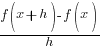 |
|
| Write the difference quotient for the given function | 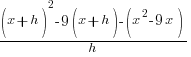 |
| Apply the exponent and use the distributive property | 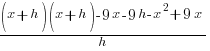 |
| Multiply | 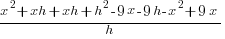 |
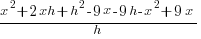 |
|
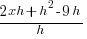 |
|
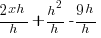 |
|
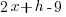 |
Example: Find the difference quotient for 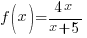
The Difference Quotient: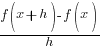
Solution:
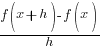 |
|
| Write the difference quotient for the given function | 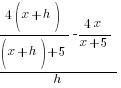 |
| Use the distributive property | 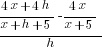 |
| Simplify the complex fraction by multiplying the numerator and denominator by the common denominator | 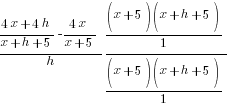 |
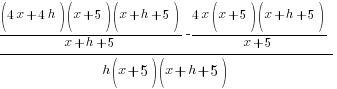 |
|
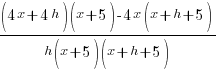 |
|
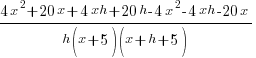 |
|
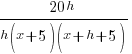 |
|
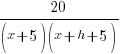 |
Example: Find the difference quotient for 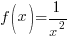
The Difference Quotient: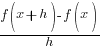
Solution:
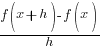 |
|
| Write the difference quotient for the given function | 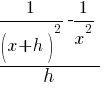 |
| Simplify the complex fraction by multiplying the numerator and denominator by the common denominator | 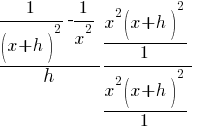 |
| Distribute the common denominator to each fraction in the numerator. | 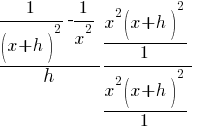 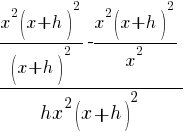 |
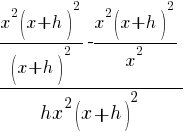 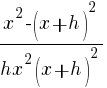 |
|
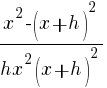 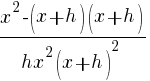 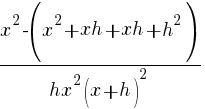 |
|
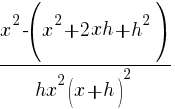 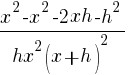 |
|
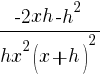 |
|
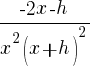 |
The difference quotient for 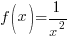 is
is