Category Archives: Algebra

1.2 Applications of Linear Equations, Applications of Linear Equations

Application of Rational Equations: Work Together (one pump stops working)

Problem:  Two pumps were required to pump the water out of a submerged area after a flood.  Pump A, the larger of the two pumps, can pump the water out in 24 hours, whereas it would take pump B 120 hours.  Both pumps were working for the first 8 hours until pump A broke down.  How long did it take pump B to pump the remaining water?

Solution:

Create a table.  List each individual and the time it takes to complete the job.  Also include a row for the pumps working together.  Use a variable to represent the unknown time to complete the job when the pumps are working together.

Time to complete the job
Pump A
  24 hours
Pump B
 120 hours
Together x

Fill in the table with the portion of the job completed in one hour.

If it takes Pump A 24 hours to complete the whole job, one twenty-forth (1/24) of the job will be completed in one hour.

If it takes Pump B 120 hours to complete the whole job, one one hundred twentieth (1/120) of the job will be completed in one hour.

If it takes x number of hours when the pumps are working together 1/x portion of the job will be completed in one hour.

Time to complete the job
  Portion completed in 1 hour
Pump A
 24 hours  1/24
Pump B
 120 hours  1/120
Together x  1/x

From here an equation can be created with the portion of the job completed in one hour.

In one hour, the portion completed by pump A plus the portion completed by pump B should equal the portion when they are working together.

1/24+1/120=1/x

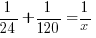
Solve the equation to find x.

 The original equation is a rational equation.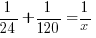
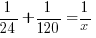1/24+1/120=1/x
Multiply the least common multiple of the denominators by each term.  The least common multiple of 24, 120 and x is 120x. 
1/24+1/120=1/x
120x(1/24)+120x(1/120)=120x(1/x)
Simplify by canceling the common factors.
 120x(1/24)+120x(1/120)=120x(1/x)
5x+x=120
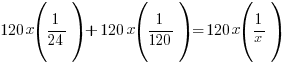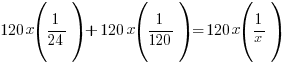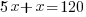Solve the remaining linear equation. 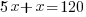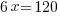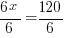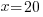5x+x=120
6x=120
{6x}/6={120}/6
x=20

It would take both pumps working together 20 hours to pump out all of the water.

But the two pumps are only working together for 8 hours which means they only get eight-twentieths (8/20) of the job done.  This fraction reduces to two-fifths (2/5).

Three-fifths (3/5) of the water remains and pump B is working alone.

It takes pump B 120 hours to complete the whole job.  It will take 120(3/5) to pump the remaining water out.

120(3/5)= 72 hours.

It takes pump B 72 hours to pump the remaining water.

5.5 Applications of Exponential and Logarithmic Functions, 6.7 Financial Models, Applications of Exponential Functions

Application of Exponential Functions: Doubling Time

Example:

How long does it take for an investment to double if it is invested at 18% compounded continuously?

Solution:

Since this question involve continuous compound interest, we will use the associated formula.

A=Pe^{rt}

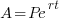
We are given that the interest rate is 18% or 0.18.  This tells me that when r=0.18 Since we are looking for the doubling time, A will be 2 times P.  I can write that in symbols A=2P.

Substitute these values into the continuous compound formula and solve for the interest rate.

Continuous compound formula
A=Pe^{rt}
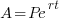Substitute the values of r and A into the formula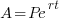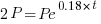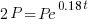
A=Pe^{rt}
2P=Pe^{0.18*t}
2P=Pe^{0.18t}
Solve for t by dividing both sides by P and simplifying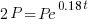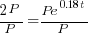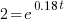
2P=Pe^{0.18t}
{2P}/P={Pe^{0.18t}}/P
2=e^{0.18t}
Solve for t by taking the log of both sides.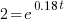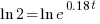
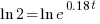2=e^{0.18t}
ln 2=ln e^{0.18t}
Solve for t by using the power rule and simplifying
ln 2=ln e^{0.18t}
ln 2=0.18t ln e
ln 2=0.18t (1)
ln 2=0.18t
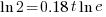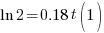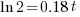Solve for t by dividing both sides by 0.18 and simplifying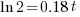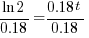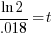
ln 2=0.18t
{ln 2}/0.18={0.18t}/0.18
{ln 2}/.018=t
Find the value in the calculator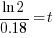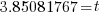
{ln 2}/0.18=t
3.85081767=t
Write the answer rounded to two decimal places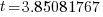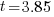
t=3.85081767
t=3.85

It will take 3.85 years to double your money when interest is compounded continuously at 18%.

If you need to write this in years and months, you will need to convert the 0.85 to months.  Since there are 12 months in a year, multiply 0.85 by 12 to get 10.2.  I will round to the nearest months to get 10.

It will take 3 years and 10 months to double your money when interest is compounded continuously at 18%.

Here is a video that is similar except that you are looking for the investment to triple.

1.5 Applications of Quadratic Equations, Applications of Quadratic Equations

Application of Quadratic Equation: Translation

Example:  The product of some negative number and 5 less than twice that number is 273.  Find the number.

Solution:  Translate the statement into an equation and then solve the equation.

“The product of some negative number…”

Let x be some negative number and multiply that number by the expression that comes next in the statement.

x  (expression that comes next)

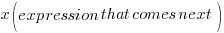
“…and 5 less than twice that number…”

5 less than means take 5 away from what follows.  Twice that number refers to 2 times the negative number that was described before.  (2x-5)

x  (2x-5)

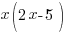
“…is 273”

This translates to equals 273.

x (2x-5)=273

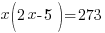
Solve the equation.

 

The translated equation
x (2x-5)=273
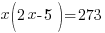Use the distributed property to rewrite the equation (recognize that the equation is a quadratic equation)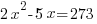
2x^2-5x=273
Choose the method for solving the quadratic equation (factoring, square root method, completing the square or quadratic formula)  I will demonstrate factoring so I need to move all terms to the same side to have zero on one side.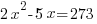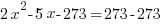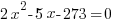
2x^2-5x=273
2x^2-5x-273=273-273
2x^2-5x-273=0
Factor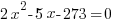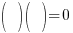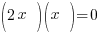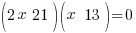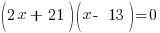
2x^2-5x-273=0
(       )(       )=0
(2x       )(x       )=0
(2x      21)(x     13)=0
(2x    +  21)(x  -   13)=0
Use the zero product property and set each factor equal to zero and solve.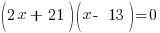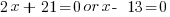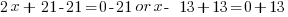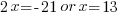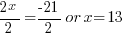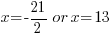
(2x    +  21)(x  -   13)=0
2x    +  21=0 or x  -   13=0
2x    +  21-21=0-21 or x  -   13+13=0+13
2x =-21 or x =13
{2x}/2 ={-21}/2 or x =13
x ={-21/2} or x =13

Since the statement says that the number is negative, the number is 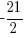{-21/2}.