All posts by admin
Analyze the Equation of an Ellipse
Example: Find the center, foci, and vertices of the ellipse. Graph the equation.
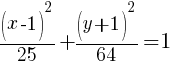
Solution:
Finding the center:
There are two standard orientations of ellipse’s, both of them have the center at (h,k).
Horizontal: 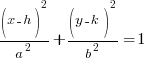
Vertical: 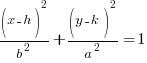
For this example the center of the ellipse is (1,-1)
Finding the orientation:
The larger denominator will indicate the orientation. Since our example has a larger denominator under the y variable the orientation is vertical. That means the ellipse is longer vertically.
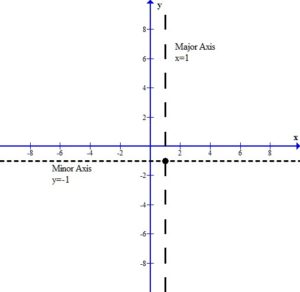
Finding the vertices: (Major Axis)
a is the distance between the center and the vertex along the major or longer axis. Since our larger denominator is 64 a is 8. I know this because the in the formula the larger denominator is 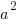 . If
. If 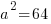 then
then 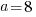 .
.
Since the ellipse is vertically oriented the vertices will be 8 units above and below the center.
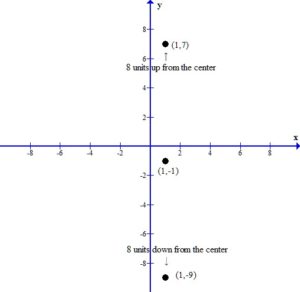
This puts the vertices at (1,7) and (1,-9).
Finding the vertices: (Minor Axis)
b is the distance between the center and the vertex along the minor or shorter axis. Since our smaller denominator is 25 b is 5. I know this because the in the formula the smaller denominator is 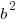 . If
. If 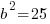 then
then 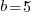 .
.
Since the ellipse is vertically oriented the vertices along the minor axis or shorter axis will be 5 units left and right of the center.
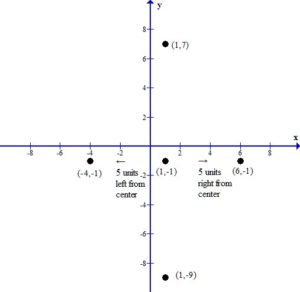
This puts the vertices at (-4,-1) and (6,-1).
Finding the foci:
c is the distance between the center and the focus. You can not find c from the equation. You must know that a, b, and c are related in a similar formula to Pythagorean theorem.
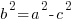
Fill in a and b, then you will be able to solve for c.
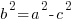
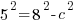
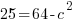
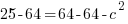
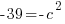
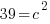
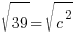
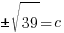
Since c is a distance we will use the positive solution. 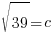 .
.
Since the ellipse is vertically oriented the foci will be 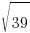 above and below the center.
above and below the center.
This puts the foci at 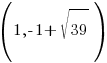 and
and 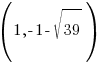
Find the equation of an Ellipse given the Foci and the Major Axis Length
Find the Equation of the ellipse given the foci and verticies
Analyze the equation of a parabola
Find the Equation of a Parabola given the vertex and a point
Rewriting the Equation of a Parabola using completing the square
Find the equation of the parabola given focus and directrix
Find the equation of a parabola given the vertex and focus
Example: Find the equation of the parabola described, find the two points that define the latus rectum, and graph the parabola.
Focus at 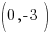 and vertex at
and vertex at 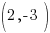
Solution:
I would like to figure out the orientation of the parabola so that I can decide which format to use when building the equation. I will put the information that I was given on a graph to help me figure out the orientation.
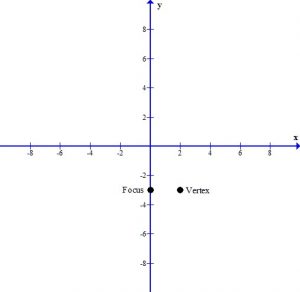
The focus is always inside the parabola and the vertex is a turning point. This tells me that the parabola must open to the left.
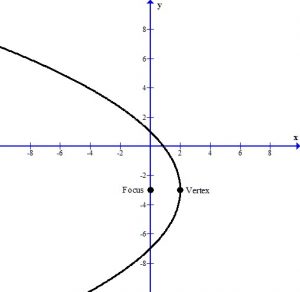
Since the parabola opens to the left, the equation of the parabola is as follows.
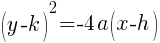
See the post about the different equations of a parabola. http://math15fun.com/2017/07/05/features-of-a-parabola/
To write the equation, I must know the vertex: (h,k) and a which is the distance between the vertex and the focus.
The vertex is given in the instructions 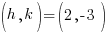 and I can find the distance between the vertex and focus by counting the units between. Thus
and I can find the distance between the vertex and focus by counting the units between. Thus 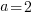 .
.
I will fill these values into the formula and simplify.
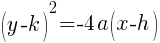
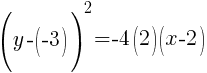
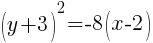
The equation of the parabola with focus at 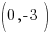 and vertex at
and vertex at 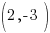 is
is
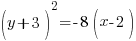 .
.
The latus rectum points are points on the parabola that are in line with the focus.
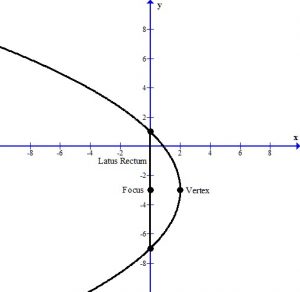
By my drawing, you notice that the two points that define the latus rectum and the focus share the same x-coordinate. This is only true when the parabola is oriented horizontally as in this example. The latus rectum points will share the y-coordinate with the focus when the parabola is vertically oriented.
The x-coordinate of the latus rectum points will be 0 and since the latus rectum points are on the parabola, I can use the equation of the parabola to help me find the rest of the ordered pairs.
Substitute a 0 in for x in the equation of the parabola and solve for y.
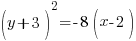 |
|
| Substitute 0 in for x and simplify. | 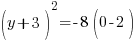 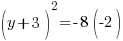 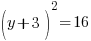 |
| Solve for y by getting rid of the square by taking the square root both sides and simplifying. | 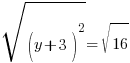 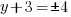 |
| Solve for y by getting rid of the plus 3 on both sides by subtracting 3 on both sides and simplifying. | 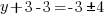 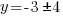 |
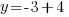 and and 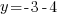 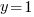 and and 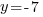 |
The latus rectum is defined by the points. 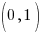 and
and 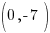 .
.
To draw the graph, place the vertex and the latus rectum points on the graph.
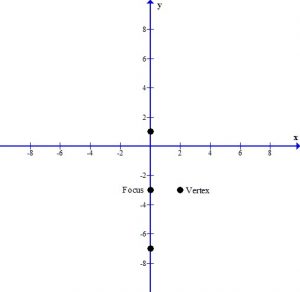
The latus rectum points show you how wide to draw the parabola.
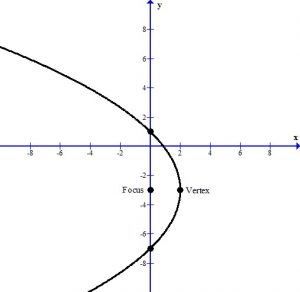
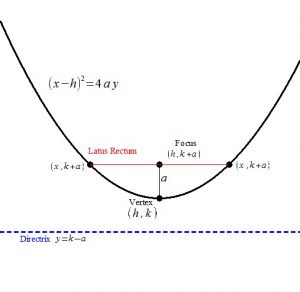
Features of a Parabola
A parabola is the set of all points P in a plane that have the same distance from a fixed point F (the focus) as they are from a fixes line D (the directrix).
Orientation: There are four main orientations of the parabola which are up, down, right and left.
Equation:
| Equation | |||
 |
Vertical orientation will have the square on the x variable. | 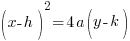 |
|
| Vertical orientation will have the square on the x variable and will have a negative because of the reflection. | 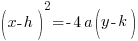 |
||
 |
Horizontal orientation will have the square on the y variable. | 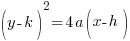 |
|
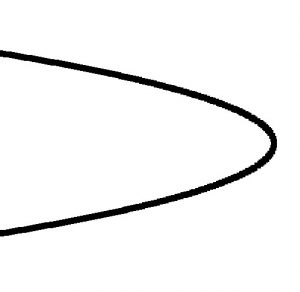 |
Horizontal orientation will have the square on the y variable and will have a negative because of the reflection. | 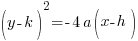 |
Features of A Parabola Oriented Up
Study the vocabulary and the location of these important features of a parabola.