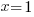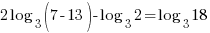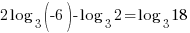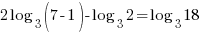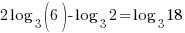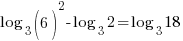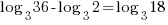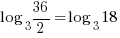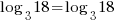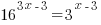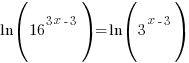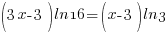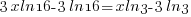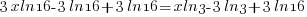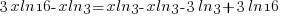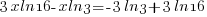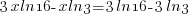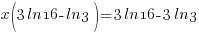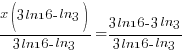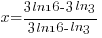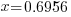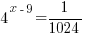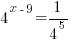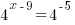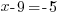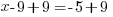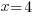Example:
What is the interest rate necessary for an investment to quadruple after 7 year of continuous compound interest?
Solution:
Since this question involve continuous compound interest, we will use the associated formula.
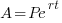
We are given that the invest quadruples in 7 years. This tells me that when t=7 that A will be 4 times P. I can write that in symbols A=4P.
Substitute these values into the continuous compound formula and solve for the interest rate.
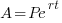 |
|
| Substitute the values of t and A into the formula | 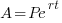 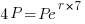 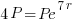 |
| Solve for r by dividing both sides by P and simplifying | 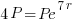 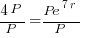 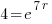 |
| Solve for r by taking the log of both sides. | 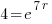 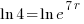 |
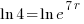 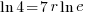 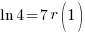 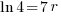 |
|
| Solve for r by dividing both sides by 7 and simplifying | 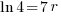 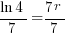 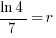 |
| Find the value in the calculator | 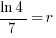 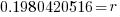 |
| Write the answer as a percentage rounded to two decimal places | 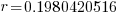 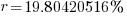 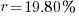 |
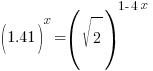
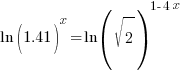
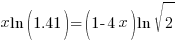
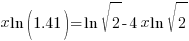
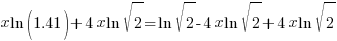
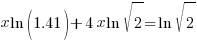
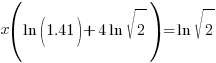
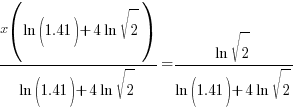
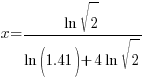
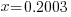
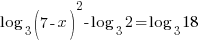
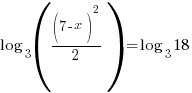
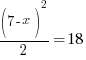
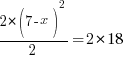
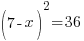
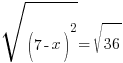
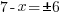
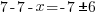
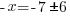
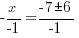
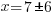
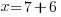 or
or 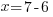
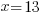 or
or