A quilt is designed in the shape of an equilateral triangle, 5 inches on each side. Each section of the quilt is in the shape of an equilateral triangle, 1 inch on a side. The sections are to alternate in color as show in the picture. How many dark green sections will be required? How many light green sections will be required?

Dark Green Sections
You can use an arithmetic sequence to represent the number of triangles in each row since the number of triangles increases by 1 in the next consecutive row.
The formula for the nth term of an arithmetic sequence is below.
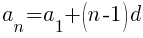
d is the common difference and 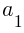 is the first term in the sequence.
is the first term in the sequence.
For the dark green sections, there is one dark green triangle in the first row and the number of dark green triangles increases by 1 in the next row. This means 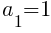 and
and 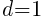
Using the formula the nth term of the arithmetic sequence is the following.
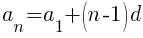
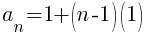
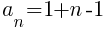
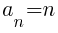
Now that the nth term of the sequence has been established we will find the sum of the rows. Each term of the sequence represents the number of dark green triangles are in that row. Summing the terms of the sequence is finding the total number of dark green triangles.
The formula for the sum of the first n terms of an arithmetic sequence is below.
![S_n=sum{i=1}{n}{{[}{{a_1+(i-1)d}}}{]}= n/2(a_1+a_n) S_n=sum{i=1}{n}{{[}{{a_1+(i-1)d}}}{]}= n/2(a_1+a_n)](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_957.5_976d6fb39024cedb0ec1dc70cd4fcf52.png)
There are five rows of dark green triangles. The sum the first five rows of dark green triangles is represented by the symbols below.
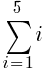
To use the formula we need the first term, the last term and n. The first term in the sequence is 1 (1 dark green triangle in the first row. The last term in the sequence is 5 (5 dark green triangles in the last row. Since there are a total of 5 rows, n is 5.
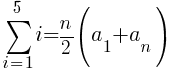
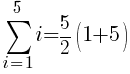
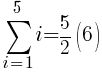
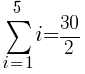
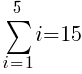
The number of dark green sections required is 15.
Light Green Sections
You can use an arithmetic sequence to represent the number of triangles in each row since the number of triangles increases by 1 in the next consecutive row.
The formula for the nth term of an arithmetic sequence is below.
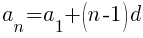
d is the common difference and 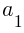 is the first term in the sequence.
is the first term in the sequence.
For the light green sections, there are no light green triangles in the first row and the number of light green triangles increases by 1 in the next row. This means 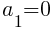 and
and 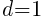
Using the formula the nth term of the arithmetic sequence is the following.
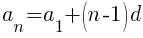
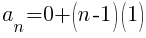
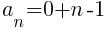
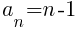
Now that the nth term of the sequence has been established we will find the sum of the rows. Each term in the sequence represents the number of light green triangles in that row. The sum of the sequence will give us the total number of light green triangles.
The formula for the sum of the first n terms of an arithmetic sequence is below.
![S_n=sum{i=1}{n}{{[}{{a_1+(i-1)d}}}{]}= n/2(a_1+a_n) S_n=sum{i=1}{n}{{[}{{a_1+(i-1)d}}}{]}= n/2(a_1+a_n)](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_957.5_976d6fb39024cedb0ec1dc70cd4fcf52.png)
There are five rows of dark green triangles. The sum the first five rows of light green triangles is represented by the symbols below.
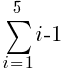
To use the formula we need the first term, the last term and n. The first term in the sequence is 0 (0 light green triangles in the first row. The last term in the sequence is 4 (4 light green triangles in the last row. Since there are a total of 5 rows, n is 5.
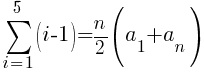
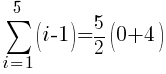
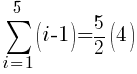
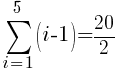
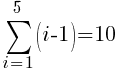
The number of light green sections required is 10.