Example: Solve the quadratic equation by factoring.
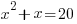
Solution:
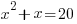 |
|
| Write the equation with all the terms on one side of the equation and zero on the other side of the equation. | 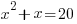 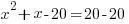 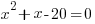 |
| Factor the expression on one side. | 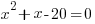 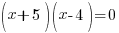 |
| Use the zero product property and set each factor equal to zero. | 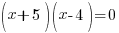 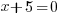 or or 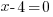 |
| Solve each equation. | 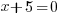 or or 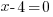 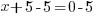 or or 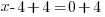 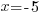 or or 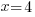 |
Check: 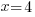
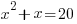
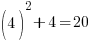
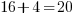
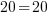
Since the value of 4 makes the equation true, 4 is a solution to the equation.
Check: 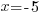
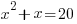
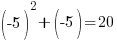
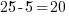
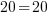
Since the value of -5 makes the equation true, -5 is a solution to the equation.