Problem: Use the Intermediate Value Theorem to show that the following function has a zero in the given interval.  Approximate the zero to two decimal places.

Solution:

To determine if there is a zero in the interval use the Intermediate Value theorem.  To use the Intermediate Value Theorem, the function must be continuous on the interval .  The function 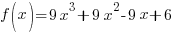 is a polynomial function and polynomial functions are defined and continuous for all real numbers.

Evaluate the function at the endpoints and if there is a sign change.  If there is a sign change, the Intermediate Value Theorem states there must be a zero on the interval.  To evaluate the function at the endpoints, calculate 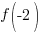  and .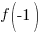

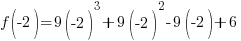
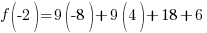
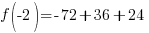
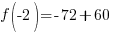
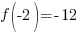
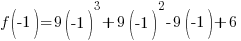
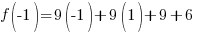
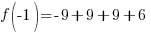
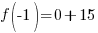
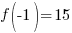
Since one endpoint gives a negative value and one endpoint gives a positive value, there must be a zero in the interval.

We can get a better approximation of the zero by trying to figure out the next decimal point. Write out all of the values to one decimal point between -2 and -1.

Fill the table.  There are functions in your calculator that make this easier.

Use the Intermediate Value Theorem again.  Look for a sign change.  Looking down the table, there is a sign change between -1.8 and -1.7.  With this information we now know the zero is between these two values.

Repeat this process again with two decimal places between -1.8 and -1.7.

Use the Intermediate Value Theorem.  Look for a sign change.  Looking down the table, there is a sign change between -1.78 and -1.77.  With this information we now know the zero is between these two values and the zero to two decimal places is -1.77 since all the numbers between -1.78 and -1.77 start with -1.77.