1.4 Quadratic Equations

Quadratic Equation: Completing the Square

Example: Solve the quadratic equation by completing the square

2x^2+8x-9=0

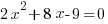
Solution:

Original quadratic equation
2x^2+8x-9=0
Move the constant to the other side of the equation by adding 9 to both sides.
2x^2+8x-9=0
2x^2+8x-9+9=0+9
2x^2+8x=9
Make the coefficient of the squared term 1 by dividing both sides of the equation by 2.
2x^2+8x=9
{2x^2+8x}/2=9/2
{2x^2}/2+{8x}/2=9/2
x^2+4x=9/2
Add the number that completes the square to both sides of the equation.  The number that completes the square can be found by starting with the coefficient of the x term, dividing by 2 and then squaring.
(4/2)^2
(2)^2
4
x^2+4x=9/2
x^2+4x+4=9/2+4
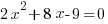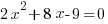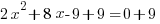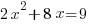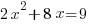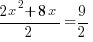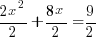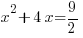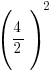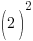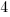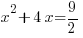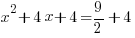The left hand side factors to be a perfect square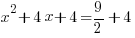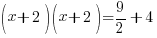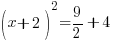
x^2+4x+4=9/2+4
(x+2)(x+2)=9/2+4
(x+2)^2=9/2+4
Simplify the right hand side by finding a common denominator and adding the fractions.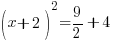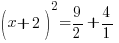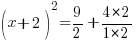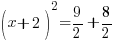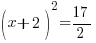
(x+2)^2=9/2+4
(x+2)^2=9/2+4/1
(x+2)^2=9/2+{4*2}/{1*2}
(x+2)^2=9/2+8/2
(x+2)^2=17/2
Solve the equation using the square root method.  Start by taking the square root of both sides to get rid of the square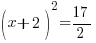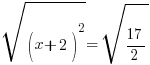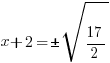
(x+2)^2=17/2
sqrt{(x+2)^2}=sqrt{17/2}
x+2=pm sqrt{17/2}
Solve for x by subtracting 2 from both sides.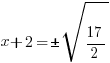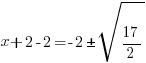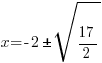
x+2=pm sqrt{17/2}
x+2-2=-2pm sqrt{17/2}
x=-2pm sqrt{17/2}
Rationalize the denominator by applying the radical to the numerator and denominator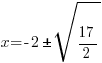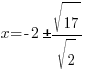
x=-2pm sqrt{17/2}
x=-2pm sqrt{17}/sqrt{2}
Rationalize the denominator by multiplying by the fraction 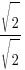 sqrt{2}/sqrt{2}
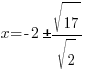x=-2pm sqrt{17}/sqrt{2}
x=-2pm sqrt{17}/sqrt{2} sqrt{2}/sqrt{2}
x=-2pm sqrt{17}/sqrt{2}
x=-2pm sqrt{34}/sqrt{4}
x=-2pm sqrt{34}/2

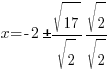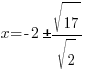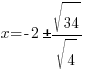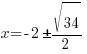https://www.youtube.com/watch?v=tHxc3fO8yOo