1.5 Applications of Quadratic Equations, Applications of Quadratic Equations

Application of Quadratic Equation: Translation

Example:  The product of some negative number and 5 less than twice that number is 273.  Find the number.

Solution:  Translate the statement into an equation and then solve the equation.

“The product of some negative number…”

Let x be some negative number and multiply that number by the expression that comes next in the statement.

x  (expression that comes next)

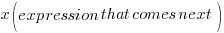
“…and 5 less than twice that number…”

5 less than means take 5 away from what follows.  Twice that number refers to 2 times the negative number that was described before.  (2x-5)

x  (2x-5)

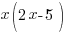
“…is 273”

This translates to equals 273.

x (2x-5)=273

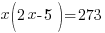
Solve the equation.

 

The translated equation
x (2x-5)=273
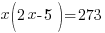Use the distributed property to rewrite the equation (recognize that the equation is a quadratic equation)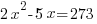
2x^2-5x=273
Choose the method for solving the quadratic equation (factoring, square root method, completing the square or quadratic formula)  I will demonstrate factoring so I need to move all terms to the same side to have zero on one side.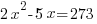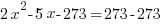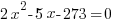
2x^2-5x=273
2x^2-5x-273=273-273
2x^2-5x-273=0
Factor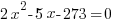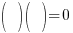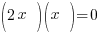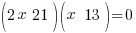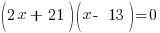
2x^2-5x-273=0
(       )(       )=0
(2x       )(x       )=0
(2x      21)(x     13)=0
(2x    +  21)(x  -   13)=0
Use the zero product property and set each factor equal to zero and solve.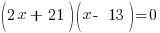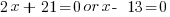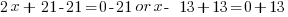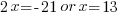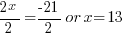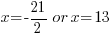
(2x    +  21)(x  -   13)=0
2x    +  21=0 or x  -   13=0
2x    +  21-21=0-21 or x  -   13+13=0+13
2x =-21 or x =13
{2x}/2 ={-21}/2 or x =13
x ={-21/2} or x =13

Since the statement says that the number is negative, the number is 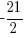{-21/2}.